![]() Résolution du système
Résolution du système
• Calculs des déplacements inconnus
Le système d'équation global à résoudre se présente ainsi :
L'application des conditions aux limites en déplacement uy1=uy4=0 consiste à :
• supprimer la première ligne et la première colonne de la matrice de rigidité globale,
• supprimer la septième ligne et la septième colonne de la matrice de rigidité globale.
Cela conduit au système suivant :
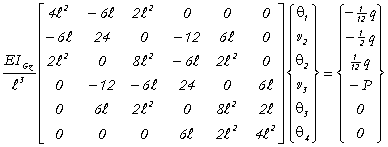
dont la résolution numérique donne :
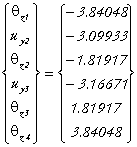
• Calcul des réactions aux appuis
Les efforts aux nuds 1 et 4 sont déterminés à partir de l'équation suivante :
![]()
Cela se résume au système suivant :
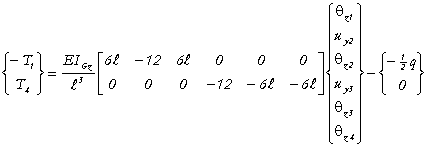
La résolution numérique donne :
![]() , où YA et YB sont les réactions aux appuis A et B.
, où YA et YB sont les réactions aux appuis A et B.
• Effort tranchant et moment fléchissant nodaux
La détermination des efforts tranchants et des moments fléchissant élément par élément sont calculés comme suit :
• Élément 1:
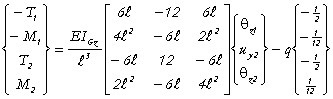
Soit :
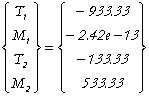
• Elément 2:

Soit :
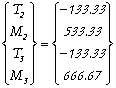
• Elément 3:
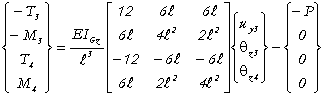
Soit :
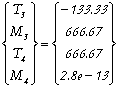
|
|
T |
Mfz |
||
|
Elément |
I |
J |
I |
J |
|
1 |
-933.33 |
-133.33 |
2.42 10-13 |
533.33 |
|
2 |
-133.33 |
-133.33 |
533.33 |
666.67 |
|
3 |
-133.33 |
666.67 |
666.67 |
2.8 10-13 |