1.2. Application à la résolution d'une équation différentielle

1.2.1. Formulation variationnelle et forme intégrale faible

On considère l'équation différentielle du second ordre :

 

 

définie sur l'espace unidimensionnel , avec les conditions aux limites de type Dirichlet : u(0)=1 et u(π)=0

La forme variationnelle forte de cette équation différentielle, selon la méthode de GALERKIN s'écrit :

 

c'est-à-dire :

 

 

où δu(x) est la première variation de u(x).

Nous obtenons par la suite la forme intégrale faible du problème en intégrant par parties le premier terme :

 

 

Cette forme se résume ainsi :

 

 

car δu(0)= δu(π)=0. En effet il ne peut y avoir de perturbations dans des valeurs constantes ou nulles.

 

1.2.2. Fonctions de forme et discrétisation

La fonction u solution de l'équation est approximée par . Nous choisissons des fonctions de forme linéaires et continues par morceaux. Sur un élément fini tel que x₁≤x≤x₂ , les fonctions de forme se présentant ainsi :

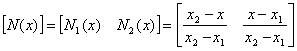
De façon plus générale :

 

La première variation de u sous forme nodale s'écrit :

De sorte que la discrétisation de la forme intégrale faible conduit à :

 

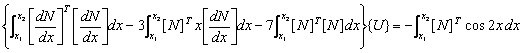
On identifie la matrice de raideur et le vecteur de charge élémentaires :

et

telles que

L'assemblage des matrices élémentaires donne la matrice globale et le vecteur global . Le système d'équation à résoudre au final est :

 

 

Au prix de quelques efforts de calculs on obtient l'expression de la matrice de raideur élémentaire, ainsi que le vecteur de charge élémentaire :

 

avec :

 

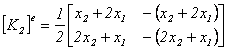
Δ=x₂-x₁ .

 

Note: Le calcul du vecteur de charge élémentaire se fait en pratique par quadrature numérique (méthode de Gauss-Legendre par exemple).