On veut résoudre numériquement sur l'intervalle ![]() l'équation différentielle suivante :
l'équation différentielle suivante :
avec les conditions aux limites ![]() .
.
La solution analytique de cette équation est :
L'approximation de la dérivée à l'aide d'une différence centrée à l'ordre 2 conduit à l'équation discrétisée :
Avec les conditions aux limites u0=un+1=0
L'espace de résolution est divisé en n+1 intervalles avec un pas de discrétisation uniforme ![]() avec
avec ![]()
En faisant varier i de 1 à n on obtient le système matriciel :

Les composantes de la matrice M et du vecteur B sont :
pour ![]() :
:
![]() ;
; ![]() et
et ![]()
Un traitement particulier est effectué pour i=1 et i=n :
![]() ;
; ![]()
![]() ;
; ![]()
![]()
![]()
Les différentes étapes conduisant à la résolution de l'équation (1) font l'objet du script en langage OCTAVE (semblable à MATLAB) contenu dans le fichier Equa_diff_finies.m. Le script est implémenté sous forme de procédure fonction recevant comme argument d'entrée le nombre N d'intervalles.
|
Equa_diff_finies.m |
|
function Equa_diff_finies (N)
endfunction
|
En appelant le script avec une valeur de N=11, on obtient la figure ci-après :
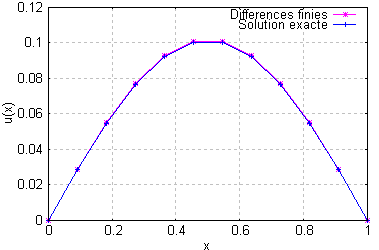
Malgré un pas de discrétisation h≈0.09, on constate que la solution discrétisée reste très fidèle à la solution analytique.