1.3.2.1. Exemple 1
Description du problème
On considère une poutre de section droite constante reposant sur deux appuis (un appuis articulé et un à rouleau), soumise à une charge uniformément répartie q sur une distance L et une charge localisée P=q.L à une distance L de son extrémité gauche (Cf. figure).
La poutre possède un module d'élasticité E=3 107Nm2, un coefficient de poisson σ=0.3, un moment quadratique IGz =549,7 10-8m4. Sa section vaut A=43 10-4m2 , avec une hauteur H=0,14 m.
On souhaite étudier la déformation de la poutre (calcul du champ de déplacement).
Modèle éléments finis de la poutre
La poutre est discrétisée en trois éléments identiques de longueur L=1m et donc quatre nœuds. La charge répartie est appliquée à l'élément 1. La charge localisée quant à elle est appliquée au nœud 3 (Cf. figure)
|
Table de connectivité
Table de coordonnées des noeuds
|
|
Noeud |
Appuis |
Condition |
Efforts |
|
1 |
rotule |
uy1=0 θ1 |
-T1 -M1=0 |
|
4 |
rouleau |
uy4=0 θ4 |
T4 M4=0 |
Matrice de rigidité globale
Les matrices de rigidité de chaque élément sont :
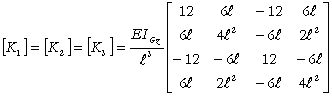
L'assemblage des matrices de rigidité élémentaires conduit à la matrice de rigidité globale :
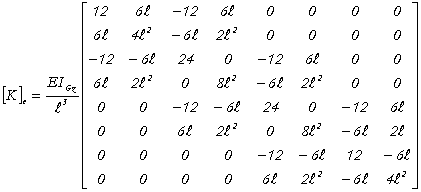
Vecteur de charge global
; 
et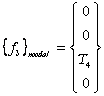 
L'assemblage de ces vecteurs donne l'expression du vecteur des forces nodales généralisé :
; 
et 
Après assemblage on a :
Le vecteur de charge global devient :
9/11 
