Les méthodes d'intégration numérique ont pour but de calculer une valeur approchée de l'intégrale d'une fonction lorsque son calcul de manière analytique apparaît laborieux voire impossible. Pour cela il faut qu'on soit capable d'évaluer en un certain nombre de points les valeurs de cette fonction.
Ces méthodes consistent à remplacer le calcul de l'intégrale par une somme pondérée prise en un certain nombre de points du domaine d'intégration.
Les deux méthodes couramment utilisées pour calculer numériquement une intégrale sont les quadratures de Gauss et celle de Newton-Cotes.
Soit à calculer l'intégrale :
Où φ(x) est une fonction de pondération assurant l'intégrabilité de f(x) sur l'intervalle [x1 x2]. Les différentes quadratures de Gauss utilisées pour calculer cette intégrale se présentent de manière générale sous la forme :
où les xi sont les zéros de polynômes orthogonaux (Legendre, Hermite, Tchebychev, etc.) affectés des poids wi et Rn le reste dû aux erreurs de troncature.
Dans la quadrature de Gauss-Legendre, on prend comme fonction de pondération φ(x)=1. Les xi sont alors les zéros du polynôme de Legendre Pn défini par la relation de récurrence:
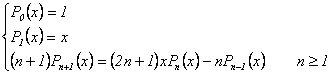
et les poids wi sont donnés par la relation :
Avec des polynômes de degré 2n-1, le reste est nulle et l'intégrale I se calcule exactement à l'aide de la relation :
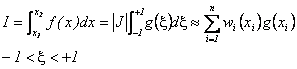
Avec 
soit 
, J est le jacobien de la transformation x-->ξ, 
et 
Dans cette méthode de quadrature, on choisit comme fonction de pondération 
sur R= 
Les xi sont dans ce cas les zéros du polynôme de Hermite Hn défini par la relation de récurrence:
où les poids wi sont définis par la relation :
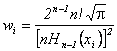
L'intégrale devient :
1/2 
