La méthode des différences est une méthode d'approximation d'équations. Cela signifie que l'équation différentielle ordinaire ou aux dérivées partielles à résoudre est approchée par une équation plus facile à mettre en œuvre numériquement. C'est le processus de discrétisation.
L'équation différentielle ordinaire du second degré qui suit nous permettra d'illustrer la démarche.
(1)
Avec 
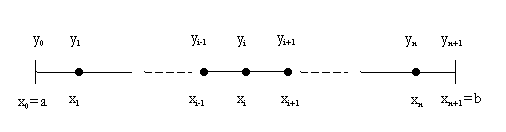
La première étape consiste à diviser (discrétiser) l'espace monodimensionnel [a ;b] en un nombre fini d'iintervalles de dimension connue (notée h et appelé pas de discrétisation). C'est le maillage.
On remplace ensuite les dérivées apparaissant dans l'équation par des quotients aux différences obtenus à partir d'un développement de Taylor à un ordre fixé selon la précision recherchée.
Si y(x) est n fois continûment dérivable sur [a ;b] alors il existe 
tel que :
(2)
On en déduit une approximation de 
à partir de ce développement à l'ordre 1 :
(3) Cette approximation de y'(x) est une différence finie décentrée en avant ou progressive à l'ordre 1.
Pour obtenir une approximation de la dérivée seconde on procède habituellement comme suit :
(2.a) 
(2.b) On additionne les relations 2.a et 2.b, ce qui conduit à :
Soit :
(4)
L'approximation de y''(x) est qualifiée de différence finie centrée à l'ordre 2.
En utilisant une combinaison linéaire de plusieurs quotients aux différences on peut construire l'approximation souhaitée avec la précision recherchée. Les tableaux suivants résument les différentes approximations des dérivées première, seconde et troisième qui apparaissent habituellement dans une équation différentielle :
|
|
yi |
yi+1 |
yi+2 |
yi+3 |
 |
-1 |
1 |
|
|
 |
1 |
-2 |
1 |
|
 |
-1 |
3 |
-3 |
1 |
|
|
yi-3 |
yi-2 |
yi-1 |
yi |
 |
|
|
-1 |
1 |
 |
|
1 |
-2 |
1 |
 |
-1 |
3 |
-3 |
1 |
|
|
yi-2 |
yi-1 |
yi |
yi+1 |
yi+2 |
 |
|
-1 |
|
1 |
|
 |
|
1 |
-2 |
1 |
|
 |
-1 |
2 |
0 |
-2 |
1 |
|
|
yi-3 |
yi-2 |
yi-1 |
yi |
yi+1 |
yi+2 |
yi+3 |
 |
|
1 |
-8 |
|
8 |
-1 |
|
 |
|
-1 |
16 |
-30 |
16 |
-1 |
|
 |
-1 |
-8 |
13 |
|
-13 |
8 |
-1 |
Par souci de simplification nous faisons le choix des notations suivantes :
et 
, etc.
En utilisant un schéma centré à l'ordre 2, les différentes dérivées apparaissant dans l'équation (1) sont ainsi discrétisées :
et 
On les substitue ensuite dans l'équation (1), ce qui nous permet d'obtenir :
Après réorganisation des éléments de l'équation discrétisée on a :
(5.a)
Cette équation discrétisée peut être réécrite sous une forme plus simple en faisant intervenir la matrice M dont les composantes sont telles que :
et 
pour 
pour 
D'où :
(5.b)
1/3 
