La logique séquentielle fait intervenir la notion de temps contrairement à la logique combinatoire. Un système est dit séquentiel lorsqu'une même combinaison des entrées peut le faire évoluer vers des états différents. Cette même combinaison peut donc engendrer des sorties différentes. En d'autres termes l'état présent du système dépend non seulement de ses entrées mais de son état antérieur. De manière générale, un système séquentiel peut se présenter ainsi:
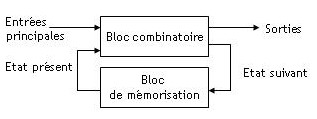
Les bascules constituent les circuits de base de la logique séquentielle. Une bascule est un circuit dont le niveau logique en sortie peut se trouver de façon durable dans deux états distincts. Cet état de sortie peut être astable, monostable ou bistable. Une bascule est dite astable quand l'état de sortie est toujours évolutif même en l'absence de signal de commande, c'est-à-dire qu'il n' y a pas d'états stables. Les bascules astables sont nommées oscillateurs ou multivibrateurs.
Une bascule peut fonctionner de manière asynchrone ou synchrone. Dans le cas synchrone l'état de la sortie est mise à jour en fonction d'un signal d'horloge.
La bascule RS asynchrone est la plus connue et la plus simple. Son symbole est représenté ci-après.
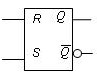
Le fonctionnement de cette bascule se traduit par deux cas suivant la combinaison des entrées qu'on souhaite utiliser pour l'effet mémoire:
|
1er cas: |
2e cas: |
|
R=0, S=0
|
R=0, S=0
|
L'entrée R (Reset) est l'entrée de mise à 0 de la sortie Q et l'entrée S (set) est l'entrée de mise à 1 de cette même sortie Q.
La synthèse de cette bascule peut être réalisée à partir de la table de vérité suivante obtenue dans le premier cas de fonctionnement:
| Entrées | Sorties | Remarques | |||
| Rn | Sn | Qn |
|
|
|
| 0 | 0 | 0 | 0 | 1 | mémoire: Qn+1=Qn |
| 0 | 0 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 1 | 0 | mise à 1 |
| 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | mise à 0 |
| 1 | 0 | 1 | 0 | 1 | |
| 1 | 1 | 0 | 0 | 0 | indéterminé |
| 1 | 1 | 1 | 0 | 0 | |
On utilise un tableau de Karnaugh pour trouver une expression simplifiée de la sortie Qn+1 en fonction des variables d'entrée Rn , Sn et Qn .
|
|
D'après donc le tableau de Karnaugh ci-contre on obtient l'expression de la sortie:
Cette expression peut être réécrite autrement de sorte a faire apparaître la fonction NOR: |
|
Cette fonction peut être réalisée avec des portes NOR à deux entrées:
Fig. 2.2.2 bascule RS à porte NOR |
La table de vérité de la bascule RS NOR se présente ainsi:
|
On la trouve implémentée dans des circuits intégrés tels que SN74LS279 ou CD4044.
La bascule RS peut dans certains cas être synchronisée par un niveau haut d'horloge, il s'agit alors d'une bascule RS synchrone nommée plus communément RSH. La table de vérité de cette bascule RSH est identique à celle de la RS quand H=horloge=1. Par contre elle reste bloquée et conserve la valeur de sortie initiale lorsque H=0.
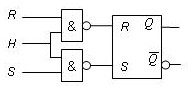
Remarque: dans le cas o ù la bascule RS est réalisée avec des portes NAND à deux entrées, l'indétermination se produit quand R=S=0 et la mémorisation quand R=S=1.
La bascule JK fonctionne comme une bascule RS synchrone mais avec un avantage essentiel, c'est- à -dire que l'indétermination qui a lieu quand R=S=1 est levée. La bascule JK maître-esclave est composée de deux étages de bascules RSH dont l'une fonctionne en maître et l'autre en esclave. Les entrées J et K jouent les mêmes rôles que les entrées S et R de la bascule RS.
|
Fig. 2.2.4 Schéma de principe de la bascule JK maitre-esclave |
Fig. 2.2.5 Symbole de la bascule RS |
Table de vérité de la bascule JK |
La table de vérité donnée ci-dessus permet d'obtenir l'équation caractéristique de la bascule JK: ![]()
La bascule JK est une bascule générique à partir de laquelle ont peut réaliser toute les autres bascules. Dans la pratique on s'en sert souvent pour faire la synthèse de compteurs ou de séquences. Dans ce cas on utilise la table de vérité dite inverse qui permet de savoir les valeurs à appliquer sur les entrées J et K des différentes bascules afin d'obtenir les transitions souhaitées au niveau des sorties.
| Qn | Qn+1 | Jn | Kn |
| 0 | 0 | 0 | x |
| 0 | 1 | 1 | x |
| 1 | 0 | x | 1 |
| 1 | 1 | x | 0 |
La bascule D ne possède qu'une seule entrée D (Data) et une horloge H pouvant être active sur front (edge triggered) ou niveau (bascule D latch). La sortie Q prend la valeur de l'entrée D lorsque le signal d'horloge est à un niveau actif ou un front actif. Par contre lorsque signal d'horloge est inactif, la sortie Q reste dans le même état quel que soit l'état de l'entrée D. La bascule D constitue un circuit de mémorisation d'une entrée de manière synchrone au signal d'horloge .
|
Fig. 2.2.6 Symbole de la bascule D edge triggered |
Table
de fonctionnement de la bascule D edge triggered |
La bascule D peut être obtenue à partir de la bascule JK (voir paragraphe 2.2.2) pour cela il suffit de poser J=D et K=/D. Les exemples de circuits représentant ce type de bascule sont SN74LS74 (TTL) et CD4013 (CMOS).
|
Exemple 2.2.1: |
|||||||||||||||||||||||||||||||||||||||
|
On voudrait remplacer la bascule JK par une bascule D. Une bascule D peut être obtenue à partir d’une JK en envoyant simultanément la même valeur sur l’entrée J et son inverse sur l’entrée K comme le montre le schéma ci-dessous :
Compléter le tableau suivant et déduire la relation liant Dn à Jn, Kn et Qn
|
|||||||||||||||||||||||||||||||||||||||
|
Solution |
|||||||||||||||||||||||||||||||||||||||
|
En se referant à la table de vérité de la bascule JK et au fait que Dn=Qn+1, on a les valeurs répertoriées dans le tableau ci-dessous:
|
|||||||||||||||||||||||||||||||||||||||
La bascule T (toggle) est une bascule dont la sortie change d'état à chaque impulsion d'horloge, c'est-à-dire que ![]() .
.
Cette expression peut être obtenue à partir de l'équation caractéristique de la bascule JK, lorsque J=K=1 (voir paragraphe 2.2.2). De sorte que la bascule T est réalisable à l'aide d'une bascule JK . On peut également réaliser une bascule T à partir d'une bascule D simplement en reliant la sortie inversée /Q à l'entrée D. Tout ceci explique pourquoi ce type de bascule n'est pas commercialisée.
|
Fig. 2.2.7 Symbole de la bascule T |
Fig. 2.2.8 Bascule D montée en T |
Table de vérité
de la bascule T |