Un ensemble contenant les éléments 0 et 1, muni des deux lois de composition internes "+ "et ".", vérifiant certaines propriétés résumées dans le tableau ci-dessous, constitue une algèbre de Boole.
| Propriétés | Théorème | Opérations |
| Elements neutres | des bornes universelles | a+0=a et a.1=a |
| Elements absorbants | du tiers exclus | a.0=0 et a+1=1 |
| Complémentation | de non contradiction |
|
| d'idempotence | a.a=a et a+a=a | |
| d'involution |
|
|
| d'absorption | a.(a+b)=a et a+(a.b)=a | |
| d'inclusion |
|
|
| de De Morgan |
|
Les opérateurs . et + sont associatifs, commutatifs et distributifs l'un par rapport à l'autre:
-commutativité: a+b=b+a ; a.b=b.a,
-associativité: (a+b)+c=a+(b+c); (a.b).c=a.(b.c),
-distributivité: a+(b.c)=(a+b).(a+c); a.(b+c)=(a.b)+(a.c)
Exemple: montrer que :
![]()
1) a + a.b=a.(1+b)=a .1 car 1+b=1
=a element neutre
2) a + /a. b=(a + a.b) + /a.b car a=a=a.b
= a + b.(a + /a) mis en facteur de b
= a + b .1 car a+ /a=1
= a + b
Les fonctions du plus simple au plus complexe peuvent être implémentée par une série d'opérateurs logiques de bases NON ET et OU auxquels on peut ajouter NON-ET, NON-OU et OU exclusif. Ces opérateurs sont aussi appelés portes logiques. Le tableau qui résume ces différents opérateurs avec leur symbole et leur équation logique:
|
Fonction |
Symbole |
Exemple de circuits |
Fonction |
Symbole |
Exemple de circuits |
|
|
NON
|
|
TTL: SN7404 CMOS: CD4049 |
OU ex (NOR)
|
|
TTL: SN7486 CMOS: CD4030 |
|
|
ET (AND)
|
|
TTL: SN7408 CMOS: CD4081 |
NON-ET (NAND)
|
|
TTL: SN7400 CMOS: CD4011 |
|
|
OU (OR)
|
|
TTL: SN7432 CMOS: CD4071 |
NON-OU
|
|
TTL: SN7402 CMOS: CD4001 |
Note: la fonction OU-ex peut être réalisée à partir de la fonction NON-ET. En effet ![]() .
.
La fonction logique traduit les relations qui existent entre les différentes variables logiques (variables binaires). Tout comme la variable logique, la fonction logique ne peut prendre que deux états logiques.
La fonction logique peut être exprimée en fonction des variables d'entrée par deux manières différentes:
-une première forme (plus usitée) o ù apparaît la somme des termes produits des variables.
Exemple: ![]()
- une deuxième forme o ù apparaît le produit des termes somme des variables.
Exemple : ![]()
Note: lorsque toutes les variables apparaissent dans la fonction logique, on parle de forme canonique ou forme normale. La forme normale est dite disjonctive si la forme canonique se présente sous la première forme (somme de mintermes) et conjonctive si elle est sous la seconde forme (produits de maxtermes).
Il arrive parfois que la fonction logique ne soit pas d éfinie pour certaines combinaisons des variables d'entrées, on dit alors qu'elle est incomplètement d é finie. On utilise un "x" pour spécifier dans sa table de vérité ou le tableau de karnaugh les valeurs non définies.
La fonction logique peut être représentée par une expression algébrique, une table de vérité, un logigramme ou un tableau de Karnaugh.
Pourquoi doit-on simplifier au maximum une fonction logique? Eh bien on le fait pour des questions de coûts de réalisation, de rapidité de fonctionnement, de fiabilité. Cela passe donc par une réduction du nombre d'opérateurs nécessaires à la réalisation de cette fonction. Diverses méthodes sont utilisées pour simplifier les fonctions logiques. Les plus utilisées sont la méthode graphique de Karnaugh et la méthode algébrique.
On parle souvent de diagramme de Karnaugh. Il s'agit d'un tableau comportant 2 n (n=nombre de variables de la fonction logique) cases qui sont telles qu'entre une case et les cases adjacentes, une seule variable logique change d'état (voir exemple). Le codage des lignes et des colonnes fait appelle au code Gray ou code binaire réfléchi. La méthode de Karnaugh devient un peu laborieuse lorsque le nombre de variables excède 6.
|
Fig. 1.3 Exemple d'un tableau de Karnaugh à 4 variables |
Le principe consiste à transcrire la fonction logique à simplifier dans le tableau et ensuite à rechercher les regroupements qui donnent une expression minimale de cette fonction, pour cela il y a quelques règles à suivre: -on regroupe les points vrais (ou faux suivant qu'on raisonne en logique négative) de la fonction qui appartiennent à des cases adjacentes, -on ne peut regrouper que 2 k (k=1,2, etc.) cases adjacentes, -on doit utiliser au moins une fois tous les point vrais de la fonction, -il est obligatoire de rechercher les regroupements les plus grands de sorte à minimiser le nombre de variables. La fonction simplifiée est la réunion de tous les regroupements, -les variables qui apparaissent dans chaque regroupement sont celles qui ne change pas quand on passe éventuellement d'une case à une autre adjacente: la variable est complémentée si elle prend la valeur 0, sinon elle reste inchangée. |
Exemple: soit à simplifier la fonction logique F dont la table de vérité est donnée ci-après:
|
|
|
Pour chaque combinaison des variables d'entrées X, Y, Z et T, on a une valeur de la fonction logique F. On transcrit ces valeurs de la fonction dans le tableau de Karnaugh et on procède aux différents regroupements (cf. tableau de karnaugh ci-dessus) selon les règles énoncées précédemment.
On obtient une forme simplifiée de F en faisant un OU logique des différents regroupements:
F= /X/ Z + /X/Y + /X/T + /Y/Z + XZT
ou
![]()
Aléas de continuité:
un alea de continuité ou de propagation peut se produire lors de l'implémentation de la fonction logique simplifiée. En effet lorsqu'un signal traverse un circuit (porte logique par exemple) il se produit un décalage par rapport au signal initial.
Pour illustrer ce phénomène, prenons la fonction logique T dont le tableau de Karnaugh est donné ci-après. Apres simplification on a![]()
,
si b=c=1 la fonction T devient ![]()
Pour implémenter cette fonction il faudra utiliser une porte logique NON avec un temps de propagation tel que la fonction T prend la valeur nulle pendant un cours instant (cf. figure).
|
|
|
|
Pour éviter les aléas de continuité il est souvent recommandé avant la réalisation de la fonction logique simplifiée, d'effectuer des recouvrements, comme celui en pointillé dans le tableau. Avec ce recouvrement la fonction T devient ![]() et prendra la valeur logique 1 quelque soit celle de a , quand b=c=1.
et prendra la valeur logique 1 quelque soit celle de a , quand b=c=1.
On simplifie la fonction logique qui est sous forme canonique en employant les règles de l'algèbre de Boole.
Exemple: soit à simplifier la fonction ![]()
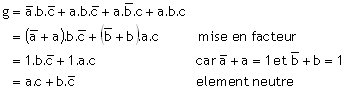
Note: la méthode algébrique s'avère quelquefois très laborieuse lorsque la fonction comporte un grand nombre de variables, de monômes (mintermes ou maxtermes).