1. Rappels théoriques

L' écoulement d'un fluide sur une plaque plane a été immensément étudié a cause de son importance théorique et pratique. La théorie de couche limite développée par PRANDTL et étudiée entre autre par H. BLASIUS pour ce qui concerne la plaque plane, a permis de d' établir un certain nombre de relations théoriques.

• Équation de Blasius

En introduisant dans les équations de Navier-Stokes, la variable de similitude et la fonction courant normalisée f(η) telle que (ψ=fonction courant satisfaisant à l' équation de continuité) BLASIUS a obtenu l' équation suivante qui porte son nom: , avec les conditions limites

 

• Épaisseur de la couche limite

La couche limite est définie de manière arbitraire comme étant l' endroit où la composante suivant x de la vitesse vaut 99% de la vitesse de l' écoulement a l' infini. Quelques hypothèses faites sur la nature de l' écoulement ont conduit à une estimation de l' épaisseur de la couche limite laminaire:

• Force et coefficient de traînée

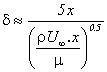
Le coefficient de traînée, dû principalement aux frottements, est défini par :

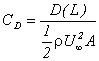
Où est la force de traînée sur toute la plaque et A=b.L= aire latérale, b= largeur et L=longueur de la plaque.

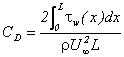
En introduisant l' expression théorique de la contrainte locale de cisaillement sur la plaque , déduite la solution de l' équation de BLASIUS, on aboutit à:

2. Description du problème

La plaque de longueur L=1m et d' épaisseur EP=2x10^-3 m, très faible comparée à sa longueur afin de moins perturber l' écoulement, est placée dans un domaine modélisé par un carré de dimension LD=2*L. Le fluide choisi est l'air à une température de 20°C avec ρ =1.205 kg.m^-3 et μ =1.8135x10^-5 Pa.s. La vitesse de l' écoulement de l'air autour de la plaque est choisie arbitrairement de telle sorte que le nombre de Reynolds reste inférieur à 10⁶ (écoulement laminaire). L'air est supposé incompressible avec des propriétés physiques constantes.

L' analyse a pour but de déterminer le profil de vitesse à un endroit de la plaque pour le comparer au profil de vitesse théorique donné par BLASIUS. On effectue également une comparaison entre le coefficient de traînée obtenu numériquement et celui calculé par la théorie.

 

3. Résultats de l' analyse

3.1. Comparaison du profil de vitesse à celui de BLASIUS

 

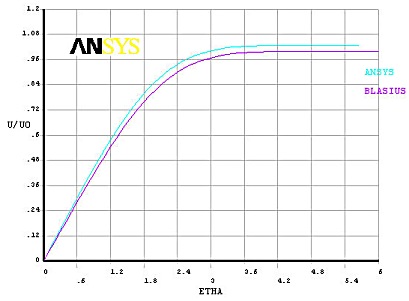
3.2. Contrainte pariétale ( τ_w )

 

 

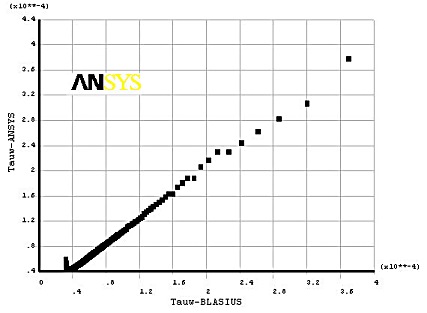
3.3. Coefficient de traînée (C_D )

La connaissance de la valeur de l'intégrale permet de déterminer la valeur du coefficient de traînée C_D. ANSYS donne:

d'ou C_D=1,93x10^-2 , soit une erreur relative de 2,5% comparée à la valeur théorique de 1,88x10^-2 donnée par la relation vue précédemment.