1. Introduction

L' écoulement autour d'un cylindre fait partie des quelques problèmes classiques de la mécanique des fluides pour lesquels les équations de Navier-Stokes admettent une solution. Ce type d' écoulement revêt un caractère pratique, parce qu'il se rencontre couramment en aérodynamique, en hydrodynamique, etc..

Le profil de l' écoulement, le coefficient de traînée (C_D), le coefficient de frottement (Cf), le coefficient de pression (Cp), sont fonctions du nombre de Reynolds base sur le diamètre du cylindre (D), la viscosité dynamique (µ), la masse volumique du fluide (ρ) et la vitesse de l' écoulement :

Selon la valeur du nombre de Reynolds, on distingue un régime d' écoulement laminaire(Re<1000) et un régime turbulent (Re>10000); et une zone de transition laminaire-turbulent (1000<Re<10000).

p=pression sur le cylindre p∞=pression à l'infini

τw=contrainte tangentielle sur le cylindre

A= aire projetée du cylindre suivant la direction de l 'écoulement

 

En fait, le coefficient de traînée tient compte de la traînée due à la pression et celle due aux frottements:

Dans le cas du cylindre la traînée due aux frottements est négligeable comparée à celle due à la pression.

 

2. Description du problème

 

L'écoulement autour du cylindre est modélisé en 2-D avec l'axe de rotation du cylindre perpendiculaire au sens de l'écoulement. Le cylindre est modélisé par un cercle de rayon R=0.05 m, situé dans le domaine représenté par un rectangle dont les dimensions sont présentées sur le la figure ci-contre. Le fluide choisi est l'air supposé incompressible à une température de 20°C avec ρ =1,205 kg.m-3 et μ =1,8135x10-5 Pa.s, constantes.

3. Résultats de l'analyse

3.1. Vortex de Karman

Pour un nombre de Reynolds Re=150, on note l'apparition de vortex de Karman dans le sillage du cylindre.

 

Visualiser l'animation

 

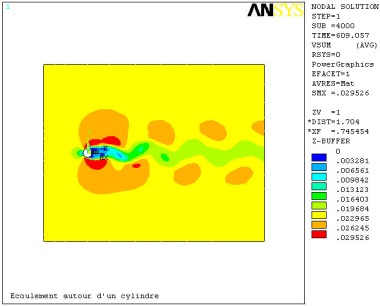
3.2. Coefficient de pression autour du cylindre et traînée à une date t

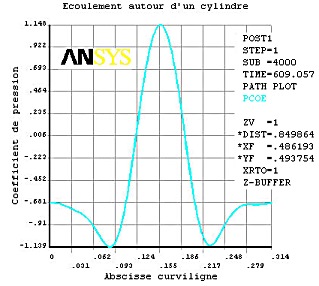
La figure ci-dessus montre l'evolution du coefficient de pression à la surface du cylindre en fonction de l'abscisse curviligne s=Rθ.

Le coefficient de traînée du cylindre à cette date a été calculé à partir de la relation suivante:

C_D=1,0006

 

Tutorial(624 Ko)

Fichier de commande