|
Une turbine est un dispositif mécanique permettant de transformer l'énergie hydraulique d'un fluide en une autre forme d'énergie (énergie mécanique). Il existe une multitude de turbines et la turbine Pelton (Lester A. Pelton (1829-1908)) en fait partie. La turbine Pelton est constituée d'une roue comportant des augets. Un jet incident sur les augets provoque la rotation de cette roue. On peut réguler la puissance mécanique en sortie sur l'arbre de la roue même si la pression motrice disponible varie. On ajuste alors au niveau de l'injecteur ou des injecteurs la vitesse du jet.
|
|
Fig. 4.2 Coupe schématique d'un auget |
Considérons la figure représentant un auget subissant un jet incident de vitesse Vj . Dans un repère mobile lie à cet auget de vitesse u=rω ( ω set la vitesse angulaire de rotation de la roue), la vitesse relative du jet est Vj - u , avec un débit massique La conservation de la matière, nous permet d'écrire d'une part:
ρSj(Vj -u)=S1V1 +ρ 2 S2 V2 (4.1)
soit puisque ρ=ρ1=ρ2 et que par hypothèse S1 = S2 =½ Sj : V1 + V2 = Vj -u (4.2a) |
Pour des raisons de symétrie et avec l'hypothèse faite que les effets de la gravité sur la trajectoire du jet après déviation sont négligeables, on a:
V1 =V2 =Vj- u (4.2b)
D'autre part le théorème de la quantité de mouvement nous permet de déterminer la force appliquée au fluide dans ce volume de contrôle:
(4.3a) La projection de la relation sur les diff é rents axes appropri é s avec le fait que 
,donne:
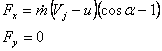(4.3b) La force qui s'exerce sur l'auget est F=-Fx c'est à dire:
(4.4)
Le couple exerc é par le jet incident sur la turbine est donc:
(4.5)
La puissance ainsi récupérée sur l'arbre de la turbine a pour expression:
(4.6)
L'équation 5.6 montre que la puissance varie de manière parabolique avec la vitesse angulaire de la roue. Et la puissance récupérée est maximale lorsque dP/dω =0 , soit quand ωmax =Vj /(2r) avec Vj=(2g ∆H)½ où ∆H est la différence de hauteur entre le niveau de la retenue d'eau et l'injecteur. Dans la pratique, à cause des pertes dans l'injecteur qui sont de l'ordre de 2% à 8%, on introduit un coefficient de vitesse Cv tel que:
Vj =Cv (2g ∆H)½ et 0.92≤Cv ≤0.98 (4.7)
La puissance hydraulique du jet incident sur la turbine est définie comme suit:
(4.8)
de sorte que le rendement de la turbine défini par η =P/PH est:
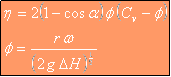(4.9)
Dans la pratique l'angle α est sensiblement égal à 165º, soit 1-cosα≈1.9659 voire 2, ce qui alors correspondrait à un angle α≈180º qui constitue un cas idéal. Le rendement maximum selon certains auteurs se produit quand Φ=½Cv ≈0.47
.jpg) Fig. 4.3 Puissance en fonction de la vitesse angulaire de rotation |
La figure 4.3 ci-contre représente l'évolution de la puissance théorique en fonction de la vitesse angulaire de la roue. Cette courbe présente un maximum tel que:
On peut alors déterminer expérimentalement la vitesse Vj et la puissance maximale, si l'angle α est connu. Sinon connaissant la vitesse Vj, on peut déterminer expérimentalement l'angle α.
|
.jpg) Fig. 4.4 Evolution du couple en fonction de la vitesse angulaire |
1/1 
, ou Qv est le débit volumique. On peut appliquer le théorème de la quantité de mouvement par rapport au volume de contrôle comme définit sur la figure. 
(4.10)