Mécanique des fluides

2.4. Calcul des forces de pression

2.4.1. Forces de pression sur une surface solide plane

Dans la vie courante, un liquide comme l'eau par exemple a besoin d' être contenu dans un récipient (contenant). Ce contenant doit alors pouvoir contenir ce liquide sans se fissurer ou se disloquer. La connaissance des forces de pression qui s'appliquent sur les parois du contenant est donc nécessaire pour son dimensionnement.
La figure 2.5.1 représente une plaque plane de forme quelconque totalement immergée dans un liquide de masse volumique ρ. La plaque est inclinée de manière arbitraire d'un angle θ de sorte que la pression qu'elle subit varie. Si on considère une surface élémentaire ds quelconque située à une profondeur h de la surface du liquide sur cette plaque, la pression qu'elle subit est P=Pa+ρgh , par conséquent une force dF telle que:

Fig. 2.5.1 Force hydrostatique sur une surface plane inclinée

(2. 5.1a )

(2. 5.1b )

car

(2. 5.2 )

La force de pression totale donc s'exerçant sur cette plaque a pour expression:

(2.5.3)

Par définition le centre de gravité G de la plaque, situé dans le plan xOy est défini par:

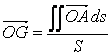(2.5.4a)

c'est à dire:

(2.5.4b)

La relation 2.5.3 peut ainsi se réécrire en tenant compte de la relation 2.5.4b:

(2.5.5a)

(2.5.5b)

L'intensité de la force exercée par le liquide sur la paroi plane est égale au produit de l'aire de la paroi par la pression effective qui règne au centre de gravité.

La force F ne s'exerce pas au centre de gravité G mais à un point appelé centre de poussée (CP). Les coordonnées du centre de poussée CP sont telles que l'intégration sur la surface totale de la plaque du moment de la force élémentaire PdS autour d'un point tel que le point O doit être égale au moment de la force de pression résultante F autour de ce même point O, c'est à dire:

(2.5.6)

(2.5.7)

Par rapport à l'axe (Ox) on a:

(2.5.8a)

(2.5.8b)

(2.5.8c)

est le moment d'inertie ou moment quadratique de la surface par rapport à l'axe de référence (Ox)

(2.5.9)

Il est souvent plus facile dans la majorité des cas de connaître le moment d'inertie par rapport à un point comme le point G, c'est à dire le moment d'inertie polaire. En appliquant le théorème de Huygens on a:

(2.5.10)

La relation 2.5.9 se simplifie aisément ainsi:

(2.5.11)

De la m ême manière, par rapport à l'axe (Oy) on a:

(2.5.12a)

(2.5.12b)

est le produit d'inertie de la surface par rapport aux axes de références (Ox) et (Oy). Ce produit d'inertie est nul si l'un des axes est axe de symétrie de la surface.

Dans la plupart des cas d'étude, la pression atmosphérique Pa agit des deux côtés de la plaque. La pression au centre de gravité de la plaque devient alors P_G =ρgh_G et celle au point A, P=ρgh de sorte que les relations 2.5.11 et 2.5.12b deviennent: