|
La grande majorité des problèmes de mécanique des fluides fait état la plupart du temps de fluide au repos. Ces problèmes concerne la répartition de la pression dans le fluide et ses effets sur les surfaces en contact avec le fluide. Cette pression P est telle que la force dF qu'elle engendre sur un élément de surface d S est normale à celle ci:
n est le vecteur unitaire normal à l'élément de surface et dirigé vers l'extérieur de la surface. Lorsque la vitesse du fluide est nulle, donc en condition hydrostatique, la variation de la pression est due seulement au poids du fluide.
|
Fig. 2.1 équilibre des forces dans un é l é ment de fluide au repos.
|
En effet, si on considère un élément de fluide au repos de volume ½ dx dy dz , comme schématisé sur la figure 2.1, aucune contrainte de cisaillement ne peut exister même suivant la surface inclinée d'un angle q. Cet élément de fluide est suppose assez petit de sorte que les pressions sont constantes sur chaque face et on peut faire l'hypothèse que les pression Px , Pz , Pn sont différentes sur chacune de ces faces.
Puisque le fluide est au repos, la somme vectorielle de toutes les forces appliquées est nulle. Suivant les axes x et y on a respectivement:
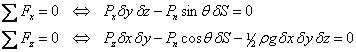 (2.1a)
(2.1a)
En tenant compte du fait que:
On obtient finalement:
La relation 2.2 illustre bien deux des principes fondamentaux de l'hydrostatique:
-la pression ne varie pas dans le plan horizontal; -la pression hydrostatique, toujours dirigée vers l'intérieur de la masse fluide, est indépendante en un point donné de l'angle d'inclinaison de l'aire sur laquelle elle agit en ce lieu. |
Considérons un élément de fluide au repos comme schématisé sur la figure 2.2. Sur les six faces de cet élément agit différentes forces dues aux différentes pressions qui y existent. En considérant que la pression P est fonction uniquement des coordonnées spatiales x, y et z, ainsi que du temps t, c'est à dire P=P(x, y,z,t), on obtient après projection sur les différents axes:
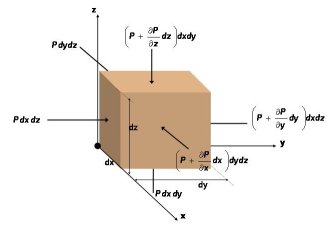
Fig. 2.2 Forces de pression sur un élément de fluide en coordonnées cartésiennes. |
|
A près simplification on obtient l'expression de la force totale exercée par la pression sur l'élément de fluide:
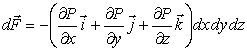 (2.4a)
(2.4a)
En remarquant que l'expression entre parenthèse dans l'expression 2.4a n'est autre qu'un gradient, on peut écrire:
En notant f la résultante totale des forces de pression par unité de volume, la relation 2.4b peut se réécrire:
Sur un é l é ment de fluide au repos comme le montre la figure 2.2, agit en dehors des forces de pression, des forces de volume dues par exemple à la gravit é ou des forces dérivant d'un potentiel. Si on considère seulement la force de gravité, à cause du poids qui est pris en compte, sur un volume élémentaire on a l'expression de cette force de gravité:
Ou tout simplement:
Dans un cas beaucoup plus général, c'est à dire si l'élément de fluide incompressible est en mouvement, on prend en compte les forces visqueuses:
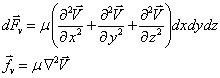 (2.6)
(2.6)
La résultante de toutes ces forces (pression, gravité et forces visqueuses) sur un élément, le met en mouvement avec une accélération a telle que:
Pour revenir au cas qui nous intéresse, c'est à dire lorsque le fluide est au repos ou a une accélération constante( a=0 ), l'équation 2.7 peut se mettre sous la forme:
f* est une force active par unité de masse. Pour un liquide soumis uniquement au champ de pesanteur, dans un repère Galiléen on a: