|
Le cas où le fluide tourne au voisinage du disque fixe fut étudié par BÖEDEWADT (1940) . L'écoulement est caractérisé par le fait que les particules en mouvement à une distance éloignée du disque fixe sont en équilibre sous l'influence des forces centrifuges et du gradient de pression radiale, tandis que celles au voisinage du disque sont animées d'un mouvement centripète et pour des raisons de continuité, ce mouvement est compensé par un écoulement du fluide vers le haut (figure 6.3). Les conditions aux limites sont différentes de celles du cas précédent: BÖEDEWADT dans son étude a fait une nouvelle hypothèse sur la pression. Il a supposé que le gradient de pression au lieu d'être axial comme dans le cas précédent est plutôt radial, c'est à dire:
 ( 6 . 12a )
où v est la vitesse du fluide : V=r ω
 ( 6 . 12b ) |
|
Avec les mêmes considérations que dans le cas précédent, il aboutit au système différentiel ordinaire :
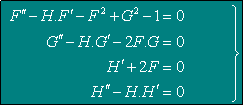( 6 . 13 )
avec les conditions aux limites suivantes:
( 6 . 14 ) .jpg)
Fig. 6.4 Distribution de vitesse au voisinage d'un disque fixe dans un fluide en rotation (source SCHLICHTING)
La figure 6.4 montre l'évolution des fonctions F, G et H obtenues après résolution numérique du système précédent. La couche limite de vitesse dans ce cas précis est deux fois plus grand que dans le cas précédent ( 
).
L'écoulement à l'infini d'un fluide incompressible au voisinage d'un disque fixe ou en rotation est un cas assez simpliste, un cas idéalisé d'une autre réalité qui est celle de l'écoulement inter disques. Ce problème qui concerne l'écoulement d'un fluide au voisinage d'un seul disque, a été généralisé à deux disques infinis par BATCHELOR (1951) avec la même transformation de similitude utilisée par VON KARMAN et BÖEDEWADT quelques années auparavant. L'écoulement entre deux disques rotatifs peut être divisé en trois cas: un premier cas où l'un des disques est fixe (rotor-stator), un second où les deux disques sont co-rotatifs et un troisième où ils sont contre-rotatifs.
L'étude faite par BATCHELOR sur ces trois configurations lui a permis de suggérer que dans le cas des disques tournant tous deux en sens inverse et à grande vitesse, une couche limite se développe sur les deux disques avec une partie centrale se comportant comme un corps solide tournant dans la même direction que le disque adjacent et dans le plan situé au milieu de l'axe des deux disques apparaît une couche de cisaillement. Dans le cas rotor-stator il a prédit également une couche limite sur les deux disques et en outre une partie centrale tournant dans le même sens que le rotor mais cette fois à faible vitesse, ce qui ne correspond pas du tout aux prédictions de STEWARTSON (1953) , qui pour sa part prévoit seulement une couche limite sur le disque en rotation. STEWARTSON prétend en outre, dans le cas rotor-stator, qu'une couche limite sur le rotor n'est pas nécessaire et qu'il ne peut y avoir de vitesse tangentielle en dehors de cette couche limite. Dans le cas de disques contre rotatifs il affirme que la vitesse tangentielle devrait être nulle en dehors des couches limites et donc que l'écoulement est purement axial. De nombreuses études tant expérimentales que numériques ont été conduites dans le but de confirmer ou d'infirmer ces observations (profil de BATHCELOR et celui de STEWARTSON ), qui sont à la base de l'une des plus pertinentes controverses de la mécanique des fluides.
SZERI & al. (1983a) ont mené une vaste étude théorique et expérimentale sur l'écoulement inter disques dans les trois configurations précédemment citées, en plus d'une autre (cas où les deux disques sont fixes). L'écoulement fondamental selon eux est caractérisé par cinq paramètres adimensionnels qui sont, le nombre de Reynolds Re=R 2 2 ω/ ν , celui basé sur le débit d'entrée RQ =Q/ 2 π ν e , le rapport des vitesses de rotation des deux disques et deux autres paramètres géométriques. Les profils de vitesse mesurées par vélocimétrie laser à effet doppler sont en bon accord avec leurs résultats numériques. Ces résultats montrent également qu'en régime permanent, le profil d'écoulement est unique et que près du milieu du rayon du disque l'écoulement est semblable à celui de BATCHELOR, résultats auxquels DIJKSTRA & al. (1983) sont aussi parvenus, de même que GAN & MACGREGOR (1995) dans le cas rotor-stator. NESREDDINE & al. ont étudié numériquement l'effet que pourrait avoir le débit d'alimentation sur le profil de l'écoulement en régime laminaire, en négligeant l'effet de perméation sur la partie du disque en rotation. Ils ont à ce propos introduit le même nombre de Reynolds basé sur le débit d'entrée que SZERI & al .. Leurs résultats montrent que l'effet d'alimentation est seulement perceptible dans la région proche de l'orifice d'entrée du fluide excepté dans le cas RQ =104 . L'augmentation du débit d'entrée influence considérablement tout le champ de vitesse entre les deux disques.
Le profil de STEWARTSON quant à lui existe seulement dans le cas de disques contre-rotatifs, quoiqu'il ait pu être observé par NESREDDINE & al. au voisinage de l'orifice d'entrée de leur système. Certains auteurs notamment BRADY & DURLOFSKY sont arrivés à la conclusion que le profil de BACTCHELOR existe dans un système clos où l'écoulement dans la cavité est séparé de l'environnement au moyen d'une chambre cylindrique, alors que le profil de STEWARTSON apparaît dans le cas où les disques ne seraient pas confinés.
Le problème classique de l'écoulement dû à un disque rotatif a été généralisé également de différentes manières dans le but de prendre en compte divers effets physiques tels que l'aspect transfert thermique [ ELLWOOD & al. (2000) , ELKINS & al. (2000) ], l'effet du champ électrique, dans le cas de fluides conducteurs [ ATTIA ] ou encore les paramètres physiques tels que la nature viscoélastique du fluide lui-même. ARIEL (1997) a considéré dans une étude théorique l'écoulement laminaire permanent, au voisinage d'un disque rotatif, d'une classe particulière de fluides viscoélastiques dénommés fluides de second degré. Il a pris en compte dans les équations de NAVIER-STOKES , l'aspect non newtonien du fluide, en introduisant un coefficient adimensionnel K ≥0 (K =0 pour un fluide newtonien) qu'il a appelé paramètre de viscoélasticité. La résolution numérique du système d'équations qu'il a obtenu, indique que plus la valeur de K augmente, c'est à dire plus le fluide est non newtonien, moins la vitesse radiale du fluide est grande et plus il y a un écoulement axial important. En outre tout semble indiquer que le cisaillement sur le disque diminue avec l'augmentation de la valeur de K .
8/10 
( 6 . 11 )