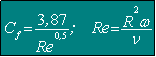L'écoulement axisymétrique laminaire permanent d'un fluide visqueux incompressible près d'un disque en rotation fait partie des quelques problèmes de mécanique des fluides pour lesquels les équations de Navier-Stokes admettent une solution unique. Von Karman (1921) fut le premier à montrer que cette équation de conservation de la quantité de mouvement se résumait en un système d'équations différentielles ordinaires non linéaires suivant les trois composantes de la vitesse en tout point. La transformation de similitude qu'il a effectuée, lui a permis de réduire la dimension spatiale à une seule dimension. Il est parvenu alors à l'aide de la célèbre méthode intégrale imaginée par lui et Paulhausen à trouver une solution approchée de ces équations. Quelques années plus tard Cochran (1934) en utilisant une combinaison de deux séries de Taylor parvient à une solution plus exacte, ce qui relevait d'un prodigieux exploit compte tenu de la méthode numérique qu'il avait utilisée. Et depuis, de nombreuses études tant expérimentales que théoriques [ ARIEL(1997), ATTIA(1998) , BRADY & DURLOFSKY (1987) , DEBUCHY & al.(1998) , HILL & al. (1999) , NESREDDINE & al.(1995) , SERRE & al.(2001) , WU & al. (2000)] , pour ne citer que ceux-l à] grâce au progrès de l'informatique ont été conduites sur cet écoulement un peu particulier, qui intervient dans les turbomachines, les viscosimètres, la lubrification, la biomécanique et aussi dans le domaine de la filtration, etc.
L'étude de l'écoulement au voisinage d'un disque à l'infinie a été faite suivant deux cas. Dans le premier cas le disque est en rotation dans le fluide au repos. Dans le second cas le fluide est en rotation et le disque est immobile. L'équation de conservation de la quantité de mouvement s'applique à ces deux cas, seules les conditions aux limites diffèrent. Les équations de Navier-Stokes et de continuité en coordonnées cylindriques deviennent alors:
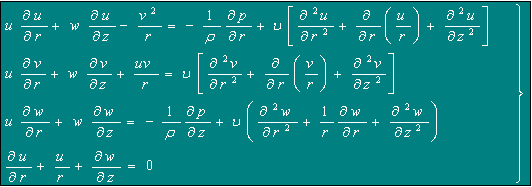 (6.1)
(6.1)
Dans le cas de l'écoulement au voisinage d'un disque en rotation dans un fluide au repos (figure 6.1), les conditions aux limites sont données par (6.2). La méthode de transformation de Karman consiste à réduire la dimension spatiale de trois à une dimension, en faisant un judicieux changement de variable (6.3), justifié par le fait que l'épaisseur de la couche limite de vitesse δ qui se développe sur le disque est proportionnelle à En faisant intervenir les fonctions F, G, H et P supposées dépendre uniquement de la variable z , les composantes de la vitesse deviennent par la suite:
La pression en tout point du fluide est supposée varier uniquement suivant l'axe de rotation z, au travers de la relation :
Les conditions aux limites deviennent, en tenant compte des transformations précédentes:
|
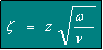 (6.3) (6.3)
|
On aboutit alors au système du second ordre fortement couplé suivant:
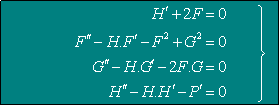 (6.7)
(6.7)
L'intégration numérique du système précédent par COCHRAN (1934) permit de connaître la valeur de la dérivée de la fonction G en zéro liée à la composante tangentielle de la vitesse [ SCHLICHTING (2000) ] et d'en déduire la valeur théorique de la contrainte de cisaillement sur le disque:
avec G'(0)=-0,616. Et le moment M des contraintes sur une face du disque est :
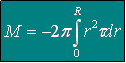 (6.9)
(6.9)
Le disque étant entièrement immergé, ses deux faces sont prises en compte et on peut introduire le moment adimensionnel:
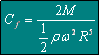 (6.10a)
(6.10a)
qui dans ce cas devient, en introduisant la valeur numérique de G'(0) :