A la controverse qui opposait BACTCHELOR et STEWARTSON vient s'ajouter le fait qu'une multitude de solutions exactes peut exister pour les mêmes équations de NAVIER-STOKES et cela aussi pour une valeur particulière du nombre d' EKMAN ( E-1=275, E= n /e 2 w ). Une pléthore d'études a été conduite dans le but de comprendre la stabilité de cet écoulement fondamental, c'est à dire en grande partie, pourquoi et comment l'écoulement devient instable et en outre quand a lieu cette transition du laminaire vers la turbulence (figure 6.5). Les premières études de stabilité ont porté sur un seul disque en rotation (configuration de VON KARMAN ) et il a été montré dans ce cas que la couche limite, couche dite d' EKMAN , car se développant sur le rotor contrairement à celle de BÖEDEWADT qui apparaît sur le stator, é tait instable et subissait plusieurs modes d'instabilités dont deux étaient connues comme étant de type I (classe B) et type II (classe A). |
Fig. 6.5 transition dans la couche limite sur un disque tournant au repos. |
L'écoulement dans cette configuration est laminaire pour un nombre de Reynolds inférieur à 4,5x104 , il devient complètement turbulent au-delà de 3,9x105 [ WU & al. ]. SZERI & al. (1983b) ont confirmé expérimentalement l'existence de l'instabilité de type I dans le cas de disques rotatifs confinés. SIRIVAT (1991) a montré expérimentalement à son tour l'existence des trois types d'instabilités, dans le cas du système rotor-stator avec un entrefer très étroit à l'inverse du système de GAUTIER & al. (1999) où l'écartement est large. RANDRIAMAMPIANINA & al. (1997) se sont préoccupés quant à eux à prédire numériquement la transition laminaire-turbulente pour le cas de disques rotatifs confinés avec une géométrie proche de celle de DAILY & NECE (1960) . L'approche numérique employé a permis de prédire avec une grande précision les deux régimes laminaires mentionnés par DAILY & NECE précédemment. La transition survient à faible nombre de Reynolds c'est à dire à environ 1,5x105 lorsque le rapport d'écartement s/R est supérieur à 0,04 selon DAILY & NECE, alors que pour RANDRIAMAMPIANINA & al., cette transition a lieu à un nombre de Reynolds compris entre 1,75x105 et 2x105 avec e/R égal à 1/11. RIAHI (1996) a pour sa part montré que la rugosité de la surface du disque en rotation avait un effet significatif sur l'amplitude des vortex apparaissant dans les différentes modes d'instabilité.
Le disque en rotation dans un espace confiné a été également étudié par KETOLA et McGRAW (1968) puis par SCHIELE (1979) [voir MURKES & CARLSSON (1988) ] suite aux travaux de DAILY & NECE . L'écoulement du fluide dans le confinement en l'absence de perméation et d'alimentation, est caractérisé par deux nombres de Reynolds dont l'un basé sur l'entrefer e et l'autre sur le rayon local r en un point donné du disque et un paramètre géométrique adimensionnel, e/r le rapport d'écartement:
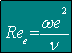 (6.15a) (6.15a) |
D'après eux quatre régimes d'écoulement peuvent être observés : Deux régimes laminaires dénommés régime I et II, deux régimes turbulents dénommés régime III et IV.
Régime I: écoulement laminaire et écartement étroit
Ce régime correspond à des valeurs de Ree ≤4 et Rer ≤ 2.105 . Les couches limites laminaires sont fusionnées (figure 6.6) et la contrainte de cisaillement varie inversement avec l'écartement e :
|
Fig. 6.6 Profil de vitesse tangentielle |
Régime II: écoulement laminaire et couches limites séparées
Ce régime correspond à Ree ≥4 et Rer ≤ 2.105 . Les couches limites laminaires se développent sur chacune des parois (figure 6.7) et la contrainte de cisaillement est indépendante de l'écartement e . Entre les deux couches se développe une zone qui tourne à la vitesse de rotation kω avec 0<k<1, où k est le coefficient d'entraînement du fluide. La contrainte de cisaillement est définie par:
|
Fig. 6.7 Profil de vitesse tangentielle dans le cas d'un large écartement |
Régime III: écoulement turbulent et écartement étroit |
|
Il correspond à des valeurs de Rer ≥2.105 et e/r ≤ 0 .05 . Le flux est caractérisé par des couches limites turbulentes qui fusionnent et la contrainte de cisaillement est définie par:
|
Ce cas correspondant à Rer ≥2.105 et e/r ≥ 0 .05 . Deux couches limites se développent sur chacune des parois, séparées par un noyau de fluide turbulent tournant à la vitesse angulaire kω . La contrainte de cisaillement est définie par :
|
|
Fig. 6.8 Différents modes d'entrée du fluide à l'intérieur de la chambre de filtration |